طريقة حساب مساحة المثلث

جدول المحتويات

هو أحد الأشكال الهندسيّة ثنائيّة الأبعاد، والتي اشتقّ اسمها من عدد أضلاعها الثلاثة، مجموع زوايا المثلث 180 درجة، ومن أنواعها

المثلّث قائم الزاوية: هو الّذي يحتوي على زاوية قياسها 90 درجة.
المثلث متساوي الساقين: هو الّذي يضمّ ضلعين لهما الطول نفسه، والثالث له طولٌ مختلف.
المثلث متساوي الأضلاع: هو الّذي أضلاعه الثلاثة لها نفس الطول، والزوايا فيه مقاسها 60 درجة.

المساحة هي قياسٌ لسطحٍ محصورٍ بين نقاطٍ معرفة، ولحساب مساحة المثلث هناك أكثر من طريقةٍ نورد أكثرها شهرةً:

طريقة العد

يمكن حساب المساحة عن طريق تقسيم المثلّث إلى وحداتٍ صغيرةٍ، مثلاً كلّ وحدةٍ تمثّل 1 مم2، أو 1 سم2، وبعد ذلك عدّها، فمجموع الوحدات يساوي مساحة المثلث.

القانون العام

لاستخدام هذا القانون يجب معرفة الآتي:

ملاحظة: في المثلث قائم الزاوية الارتفاع هو طول الضلع الثاني المجاور للقاعدة، ويشترك معها في تشكيل الزاوية القائمة.

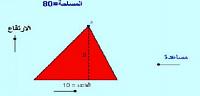
المساحة = ½ القاعدة × الارتفاع

مثال: تعرف على ما هى مساحة مثلثٍ ارتفاعه 10 سم: وطول قاعدته 5 سم؟ المساحة = ½ × 10 × 5 = 25 سم2.

قانون المساحة بمعرفة طول الأضلاع الثلاثة

يمكن حساب المساحة للمثلّث عند معرفة أطوال الأضلاع الثلاثة باتباع الطرق وخطوات التالية:

نقوم بحساب المحيط = مجموع طول الأضلاع.
نقوم بحساب المعامل هـ = المحيط / 2
نطبق المعادلة التالية: المساحة = الجذر االتربيعيّ (هـ(هـ - طول الضلع الأول) (هـ - طول الضلع الثاني) (هـ- طول الضلع الثالث))

مثال: مثلث أطوال أضلاعه 3 سم، 5 سم ، 4 سم، تعرف على ما هى مساحته؟

محيط المثلث = مجموع أطوال أضلاعه = 3 + 5 + 4 = 12 سم.
المعامل هـ = المحيط/ 2 = 12/2= 6 سم.
المساحة = الجذر االتربيعي (هـ(هـ - طول الضلع الأول) (هـ - طول الضلع الثاني)(هـ- طول الضلع الثالث))

= الجذر التربيعي(6(6-3)(6-5)(6-4)) = الجذر التربيعي (6(3)(1)(2)) = 6 سم2

قانون المساحة للمثلّث متساوي الأضلاع

المساحة = الضلع 2× (الجذر التربيعي 3) / 4

مثال: مثلّث متساوي الأضلاع طول ضلعه 3 سم تعرف على ما هى مساحته؟

المساحة = 3 2 × الجذر التربيعي (3)/4 = 3.89 سم 2

قانون المساحة بمعرفة طول ضلعين وزاوية محصورة بينهما

المساحة = ½ طول الضلع الأول × طول الضلع الثاني × جا هـ

مثال : ما مساحة المثلث إذا كان طول الضلع الأول 6 سم، والضلع الثاني 5 سم، والزاوية المحصورة بينهما 30 درجة؟

الحل: المساحة = 1/2×6×5×جا30.

= 1/2 × 6 × 5 × 1/2 =7.5 سم 2

قانون المساحة بمعرفة طول ضلع وزاويتين

لا يمكن تطبيق قانون المساحة مباشرةً، لذا نلجأ إلى استخدام المعادلات التالية لمعرفة أطوال الأضلاع الأخرى.

ومنه يتمّ حساب مقاس الزاوية الثالثة.

قانون الجيب = طول الضلع الأول / جا الزاوية المقابلة له= طول الضلع الثاني / جا الزاوية المقابلة له = طول الضلع الثالث / جا الزاوية المقابلة له، بعدها يتم حساب المساحة باستخدام قانون المساحة بمعرفة أطوال الأضلاع الثلاثة، أو قانون المساحة بمعرفة طول ضلعين والزاوية المحصورة بينهما.

مواضيع ذات صلة بـ : طريقة حساب مساحة المثلث