جدول المحتويات
الدائرة
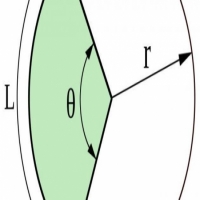
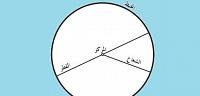
الدائرة هي أحد الأشكال الهندسية وهي عبارة عن نقاط متصلة ببعضها البعض وبعيدة بعد ثابت عن نقطة ما تسمى مركز الدائرة، وإذا رسمنا خطا من مركز الدائرة إلى أي نقطة من النقاط المتصلة يتشكل لدينا ما يسمى بـ (نصف القطر)، أما الخط الواصل بين أي نقطة من النقاط المتصلة إلى أي نقطة أخرى من هذه النقاط ومارا بنقطة المركز فيسمى (قطر الدائرة). سنعرض في هذا المقال قانون محيط الدائرة ومساحتها.
قانون محيط الدائرة ومساحتها
محيط الدائرة
- محيط الدائرة: هو طول الخط الذي يحيط بالشكل الهندسي، وهو هنا الدائرة.
- قانون محيط الدائرة: يساوي طول القطر (المعرف أعلاه في المقدمة)×(باي أو ط)، وهي تساوي 3.14 أو 22/7، وهنا سنضع مجموعة من الأمثلة للتوضيح:
أمثلة تطبيقية للقانون:
- إذا علمت أن قطر عجلة مركبة يساوي 50 سم، احسب محيط العجلة.
أوجد محيط دائرة بالـ (سم) إذا علمت أن نصف قطرها يساوي 10 م.
- بداية نجد طول القطر، وهو 10×2=20 م.
- نحول الآن وحدة القطر إلى الوحدة المطلوبة وهي السنتيمتر، عن طريق ضرب طول القطر في 100، إذا 20م×100=2000 سم.
- وبذلك نحصل على النتيجة، وهي أن محيط الدائرة=2000×3.14=6280 م.
أوجد طول قطر دائرة محيطها يساوي 450 سم.
- محيط الدائرة=طول القطر×3.14، إذا طول القطر=محيط الدائرة / 3.14.
- إذا وبتطبيق القانون أعلاه فإن طول القطر=450 / 3.14 ويساوي تقريبا 143.3 سم.
مساحة الدائرة
- هي قياس منطقة محصورة في حدود معينة (المنطقة المحصورة في محيط الدائرة).
- قانون مساحة الدائرة يساوي (باي أو ط)×نق تربيع (أي نصف القطر×نصف القطر).
أمثلة تطبيقية لقانون مساحة الدائرة:
إذا علمت أن قطر دائرة يساوي 40 سم، أوجد مساحة الدائرة.
- بداية نجد طول نصف القطر، وهو 40/ 2=20 سم.
- بتطبيق القانون أعلاه فإن مساحة الدائرة=3.14×20 تربيع=3.14×20×20=1256 سم.
أوجد قطر دائرة، إذا علمت أن مساحتها تساوي 5.024 سم.
- إذا كانت المساحة=3.14×نق تربيع، فإن نق تربيع=المساحة/ 3.14، إذا نق تربيع=5.024/ 3.14=1600 سم.
- نق تربيع=1600 سم، نق=جذر الـ 1600 ويساوي 40.
- إذا كان نق=40، فإن القطر=40×2=80 سم.
أوجد مساحة دائرة بالمتر، إذا علمت أن نصف قطرها يساوي 20 سم.
- نصف القطر تربيع يساوي 20×20=400 سم.
- بتحويل السنتيمتر إلى متر فإن نق تربيع=400 سم/ 100=4 متر.
- نعود إلى قانون المساحة ويساوي 3.14×نق تربيع ويساوي 3.14×4=12.56م.