الشكل المضلّع هو ذلك الشكل ثنائي الأبعاد، وهو أساس الأشكال الهندسيّة كلّها، وهو شكل يتكوّن من اتحاد عدد من القطع المستقيمة بجانب بعضها البعض، ممّا يشكل شكلاً مغلقاُ يسمّى بهذا الاسم. تسمّى كل قطعة مستقيمة تُكوّن هذا الشكل بالضلع، أمّا كل زاوية تكون محصورة بين كل ضلعين متجاورين في الشكل المضلّع فتسمّى زاوية المضلّع. الأشكال المضلّعة تسمّى بعدد أضلاعها، ولعمل شكل مضلّع يتطلّب وجو ثلاثة أضلاع تشكّل مع بعضها البعض شكلاً مغلقاً، وهذا الشكل ذو الأضلاع الثلاثة يسمّى المثلّث، أمّا إن تكوّن المضلّع من أربعة أضلاع فإنّه يسمّى شكلاً رباعيّاً، وإن تكوّن من خمسة أضلاع يسمّى الشكل الخماسي وهكذا.
الأشكال الرباعيّة لها أنواع متعدّدة، من هذه الأنواع ومن أبرزها الشكل المتوازي الأضلاع، وهو الشكل الذي يمتاز بتقابل كل زاويتيتن فيه مع بعضهما البعض حيث تكون هاتان الزاويتان متساويتين، ومن خصائص هذا الشكل الثنائي الأبعاد الأخرى أن كل ضلعين من أضلاعه متقابلين يكونان متساويان أيضاً، وللشكل المتوازي الأضلاع حالات خاصة عديدة ومتنوعة نورد منها ما يلي
الشكل المعين
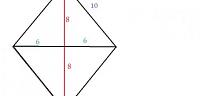
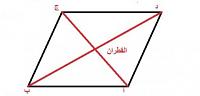
يعتبر الشكل المعين واحداً من الأشكال الرباعيّة، وهو شكل يمتاز بأن أضلاعه الأربعة متساوية، بالإضافة إلى أنّه كما في المتوازي فإنّ كل زاويتين متقابليتن فيه تكونان متساويتين، أيضاً أقطار المعين متعامدة، وكل ضلعين من أضلاعه متقابلين هما متوازيين. أمّا بالنسبة للأقطار، فإنهما يتعامدان معاً في منتصفيهما. ويشبه المعين في شكله الألماس.
محيط المعين يساوي مجموع أطوال أضلاعه، أمّا مساحته فهي تُعطى بالعلاقة التالية: (مساحة المعين = 0.5 * القطر الأول * القطر الثاني)، فمثلاً لو كان لدينا معين طول قطره الأول يساوي (30 سم ) أمّا طول القطر الثاني فيساوي (25 سم)، وأردنا إيجاد المساحة، فإننا ببساطة نضرب أطوال الأقطار فيكون الناتج (750) ومن ثم نقسم الناتج على (2) لينتج العدد (375) سم مربعاً. أمّا لو كان لدينا معين طول ضلعه (50 سم) وأردنا حساب محيطه فببساطة شديدة نضرب طول الضلع الواحد بأربعة ليكون الناتج هو 200 سم، حيث إنّ أطوال أضلع المعين كلها متساوية، فيلزمنا فقط طول ضلع واحد لإيجاد طول المحيط.
المربع والمستطيل
المربع والمستطيل هما من الأشكال الأخرى غير المعين اللذان يشكّلان حالة خاصة من متوازي الأضلاع، ويتميّزان بأنّ زواياهما الأربعة قائمة، وأنّ الأضلاع المتقابلة متوازية، إلا أنّهما يختلفان في أطوال الأضلاع، فأطوال أضلاع المربع متساوية في حين أن كل ضلعين متقابلين متساويين في المستطيل. وهما أيضاً من الأشكال الهندسية الهامة.