جدول المحتويات
خصائص المثلث
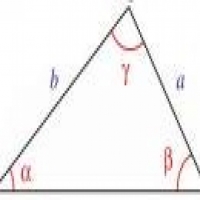
يعتبر المثلث من الأشكال الهندسية المنتظمة، وله ثلاثة أضلاع موصولة مع بعضها البعض، والتي قد تكون متساوية أو متفاوتة في طولها، وتحصر فيما بينها زوايا إما أن تكون حادة أو قائمة، وتتشارك جميع المثلثات بشكل عام في مجموعة من الصفات والخصائص، وهي عدد الأضلاع، مجموع الزوايا الداخلية له والتي يجب أن تساوي 180 درجة، ولكن في هذا المقال سوف نتطرق ووسائل إلى خصائص المثلثات بشكل مفصل.
خصائص المثلث قائم الزاوية
- أطلق على المثلث اسم قائم الزاوية لأنه يحتوي على زاوية قائمة (90 درجة).
- يطلق على الضلع المقابل للزاوية القائمة اسم الوتر، ففي الثلث (أ، ب، جـ) والقائم في (ب)، فإن الوتر هو الضلع (أ جـ).
- مجموع الزوايا المتبقية في (أ) وفي (ب) يجب أن تساوي 90 درجة، بحيث عندما يتم جمعها مع الزاوية القائمة، يتم الحصول على 180 درجة.
- يطلق على الزوايا (أ) و(ب) اسم الزوايا المتتامة.
- عندما يتم إنزال عمود من رأس الوتر، فإن قياس هذا العمود يساوي نصف طول الوتر.
- تعتبر الزاوية القائمة هي النقطة التي تجتمع فيها جميع ارتفاعات الأضلاع.
- يمكن إيجاد أطوال أضلاع المثلث قائم الزاوية من خلال اتباع نظرية فيثاغوروس، والتي تتضمن ما يلي: (طول الوتر) مربع = (طول الضلع الأول) تربيع+ (طول الضلع الثاني) تربيع.
- هناك نوع من المثلثات قائمة الزاوية، والتي تساوي فيه الزوايا (أ) و(ب) 60 درجة و30 درجة.
- يعتبر المثلث متساوي الساقين في بعض الحالات مثلثا قائما.
خصائص المثلث متساوي الأضلاع
- يعتبر المثلث متساوي الأضلاع حالة خاصة من المثلثات متساوية الساقين.
- تعتبر جميع المثلثات التي تتساوى أضلاعها مثلثات متشابهة، ولكنها ليست متماثلة.
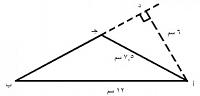
- يطلق على العمود النازل من رأس المثلث إلى القاعدة اسم الارتفاع، والذي ينصفها إلى قطعتين متساويتين.
- يكون ارتفاع المثلث عموديا على القاعدة، بمعنى أنه يشكل زاوية قائمة معها.
- تكون جميع زوايا المثلث متساوي الأضلاع متساوية، وتبلغ قيمتها 60 درجة.
- يحقق شروط نظرية فيفياني، والتي تنص على أنه في حالة تم وضع نقطة في منتصف المثلث متساوي الأضلاع، وكان هناك خط واصل ما بين كل ضلع والنقطة، فإن مجموع الخطوط الثلاثة الناتجة يكون مساويا لطول ارتفاع هذا المثلث.
خصائص المثلث متساوي الساقين
- هو المثلث الذي يتساوى فيه طول ضلعين على الأقل.
- يطلق على الضلع المتبقي من المثلث اسم القاعدة.
- يطلق اسم (النقطة) على الرأس المقابل للقاعدة.
- تتساوى زوايا قاعدة المثلث متساوي الساقين.
- تندرج زوايا المثلث متساوي الساقين تحت مسمى الزوايا الحادة، وهي الزوايا التي تكون أكبر من 0 وأقل من 90 درجة.
- يطلق على العمود الواصل ما بين رأس المثلث وقاعدة المثلث اسم الارتفاع، والذي يكون عموديا على القاعدة، كما أنه ينصف الزاوية الرأسية.