المثلث
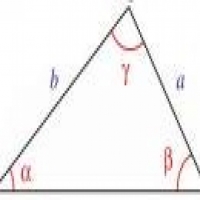
يعتبر المثلث واحدا من الأشكال المغلقة الأساسية التي يتم استخدامها في مجال الهندسة، وهو عبارة عن شكل ثلاثي الرؤوس والأضلاع التي تشكل قطعا مستقيمة، ومن ضمن أحد الشروط التي يجب أن تكون في المثلث هي أن يكون طول أحد الأضلاع أقل من مجموع طول الضلعين الآخرين، وقد تم تصنيف المثلثات بناء على طول أضلاعها إلى ثلاثة أقسام وهي: المثلث متساوي الأضلاع، ومتساوي الساقين، بالإضافة إلى المثلث صاحب الأضلاع المختلفة.
هناك معيار آخر تم اعتماده في تقسيم المثلثات وهو قياس زواياه (المنطقة داخل المثلث والمحصورة ما بين ضلعين)، فيوجد هناك المثلث حاد الزاوية؛ والتي تكون جميع زواياه أقل من 90 درجة، والمثلث المنفرج؛ والذي تكون قياس زواياه أكبر من 90 درجة، ولكن في الوقت نفسه يجب ألا تزيد عن 180 درجة، وأخيرا هناك المثلث صاحب الزاوية القائمة؛ والتي تساوي 90 درجة، ومن الجدير بالذكر بأن مجموع الزوايا الداخلية لأي مثلث يجب أن تساوي 180 درجة.
مثلث قائم الزاوية
هو واحد من أنواع المثلثات، والذي يمتاز بمجموعة من الخصائص التي يمكن أن نلخصها في النقاط التالية، وهي:
- قيمة إحدى الزوايا الداخلية فيه تساوي 90 درجة.
- يطلق على ضلع المثلث الذي يقابل الزاوية القائمة اسم وتر المثلث، فعلى سبيل المثال لو كان لدينا المثلث (أ ب ج)، وكانت زاويته القائمة هي (ب)، سيكون الضلغ (ج أ) هو الوتر.
- يحتوي على زاويتين متتامتين بمعنى أنه إذا كانت الزاوية القائمة هي (ب)، فهذا يعني بأن مجموع الزاويتين أ و ج يجب أن يساوي 90، وذلك انطلاقا من القاعدة التي تنص على أن مجموع زوايا المثلث يجب أن تساوي 180 درجة.
- هو المثلث الوحيد الذي تنطبق عليه نظرية فيثاغوروس.
وتجدر الإشارة إلى أنه تم تقسيم مثلث قائم الزاوية إلى ثلاثة أنواع وهي: مثلث قائم الزاوية ولكن متساوي الساقين، بالإضافة إلى المثلث الذي يحتوي على زاويتين قياسهما 30 و 60 درجة، ومثلث كيبلر.
العمليات الحسابية الخاصة بالمثلث القائم الزاوية
مساحة المثلث قائم الزاوية
نستطيع أن نحسب مساحة المثلث القائم من خلال اتباع القاعدة التالية وهي: (طول قاعدة المثلث * ارتفاع المثلث)/2، ففي حالة المثلث (أ ب ج) والقائم الزاوية في ب، يعتبر الضلع (أ ج) هو الوتر، فإذا قمنا بمد خط من الزاوية (ب) على الوتر، فيكون هذا الخط هو ارتفاع المثلث، ويكون الوتر هو القاعدة.
قانون محيط المثلث قائم الزاوية
أما لحساب محيط المثلث (أ ب ج) ما علينا إلا أن نقوم بجمع أطوال الأضلاع الثلاثة حسب القانون التالي: محيط المثلث = أ ب + ب ج + ج أ