الإنسان بدوره يحب الاستكشاف والمغامرة ، فلطالما استهوته المساحة المستوية بكل أشكالها ، فعرف أول ما عرف النقطة ، وهي شكل ليس له أبعاد البتة ، فلا طول له ولا عرض ، ثم تطور به الحال ، فعرف الخط المستقيم ، ثم عرف الشعاع ، فالقطعة المستقيمة ، وهذه تسمى أشكال أحادية البعد ، أي أنها تتكون من طول فقط ، ثم ارتقى العقل البشري ، وأراد أن يحيط الأراضي ، فاستخدم الهندسة المستوية ، وهي ما تصنف تحت الاشكال ثنائية الابعاد ، فعرف منها المثلث بأشكاله على انه أبسط شكل ثنائي الابعاد من حيث عدد اضلاعه وشكلها ، إذ يتكون من ثلاث اضلاع مستقيمة مكونة شكلا مستويا مغلقا ، ثم عرف الشكل الرباعي بأشكاله وألوانه ، وهو ما يتكون من اربعة اضلاع ، ثم عرف الخماسي والسداسي والسباعي والثماني والتساعي والعشاري ، وهلم جرا .
لكنه في الجانب الآخر بعد النقطة تعرف على الخط المنحني والمنحنى المغلق والقوس ، وهذه الأشكال مع أنها غير مغلقة إلا أنها ثنائية الأبعاد ، يأتي بعدها الدائرة والقطاع الدائري والقطعة الدائرية والشكل البيضاوي والشكل الإهليجي والقطع الناقص والقطع المكافئ وغيرها .
وها نحن الآن نسلط الضوء على الدائرة ، ويمكننا تعريفها بانها جميع النقاط التي تبعد عن نقطة ما نفس المسافة بشرط أن تكون جميعها في مستوى واحد .
هذا ، وتتميز الدائرة بالخواص التالية :
- شكل هندسي .
- شكل مغلق .
- شكل ثنائي الأبعاد .
- يتكون من قوسين مغلقين .
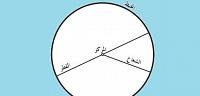
- يتحدد بمعرفة قطره ، وقطر الدائرة هي أكبر مسافة بين نقطتين على محيطها ، ويجب أن يمر بمركزها الذي ينصف أقطارها كلها .
- للدائرة عدد لا نهائي من الاقطار.
- لها عدد لا نهائي من محاور التماثل .
- النسبة دائما بين محيط أي دائرة وقطرها هو عدد ثابت ، ويسمي ثابت الدائرة ورمز له بالرمز ط ويقدر ب (22÷7) أو 3.14 .
- محيط أي دائرة هو حاصل ضرب هذا الثابت في قطرها ، أي بالرموز محيط الدائرة = ط*ق=2*ط*نق، علما بأن : ق رمز لقطر الدائرة ويساوي ضعفي نصف قطرها ، وان نق هو نصف قطر الدائرة ، وط هو رمز ثابت الدائرة = 3.14 تقريبا .
- مساحة الدائرة تساوي ثابت الدائرة في مربع نصف قطرها ، وبالرموز مساحة الدائرة =ط*نق 2.
أما الطريقة العملية لإيجاد محيط ومساحة دائرة على أرض الواقع ، بشرط معرفة مركزها فيتم كما يلي :
- نضع شاخص في مركز الدائرة .
- نضع شاخص على أي نقطة على حدود الدائرة .
- نقيس المسافة بينهما .
- نطبق قانون المحيط ، وهو محيط الدائرة = 3.14 * 2 * نق .
- نطبق قانون المساحة ، وهو مساحة الدائرة = 3.14*نق *نق .
لاحظ أخي القارئ أن الفرق بين الدائرة والشكل الإهليجي ان الشكل الإهليجي مكون من مركزين وبينهما مسافة معينة ، بينما هو الفرق بين الدائرة والقطع الناقص أن القطع الناقص أشبه باتحاد قوسين متماثلين ومتعاكسين في الاتجاه ، بحيث لا يكون مجموع زاويتيهما 360 درجة ، وبذلك يمكننا اعتبار الدائرة حالة خاصة من الشكل الإهليجي ، وذلك إذا اعتبرناها شكلا إهليجيا والمسافة بين مركزيه صفر ، وهي _ أي الدائرة _ حالة خاصة أيضا من القطع الناقص ، إذ تكون فيها قياس كل زاوية من زاويتي القوسين المركزيتين 180 درجة ، فيصبح مجمعهما 360 درجة .
بهذا يمكننا إيجاد محيط و مساحة أي دائرة على أرض الواقع ، وبطريقة عملية وعلمية مبسطة وسهلة للغاية .