بعد الانتشار الكاسح لعلوم الرياضيات في العصر الحديث وتواجدها في كل ساحة من ساحات الحياة وفي كل تخصص من التخصصات التي تدرس في الجامعات، ومع تزامنه مع علم الهندسة الهادف إلى حساب كل من الأطوال والمساحات والأحجام، كان لا بد من إيجاد مساحات الأشكال الهندسية الأساسية التي تنتمي إلى المستوى الفراغي الثاني (المستويات) والتي يمكن التعبير عنها بالكثير من المصطلحات أشبه ما تكون بالمربع والمستطيل وغير ذلك من الأشكال التي يبنى عليها الكثير من القوانيين الهندسية والرياضية في العلوم المختلفة كالميكانيكا الخاصة بالتربة أو صناعة الآلات أو تحليل الأحمال وإلى ما ذلك من الحساب ومنه أيضا حساب مساحات الأراضي وغير ذلك.
تعتبر عملية إيجاد المساحات مسألة بسيطة جدا وغير معقدة تعتمد في أصلها على إيجاد المحيط الخارجي الذي يحتوي مساحة معينة من الأرض وغالبا ما يدلل على التكامل هو مساحة الأشكال الهندسة والتي تعطي الإنطباع الخاص بها، فيمكن التعبير عن تكامل قيمة معينة بمجموع مساحات شكل معين، وهذا يذهب بنا إلى الأصل في طريقة إيجاد مساحات الأشكال ولنفترض أننا نمتلك مربعا معينا مكون من أربعة أضلاع طول كل واحد منها عبارة عن 1 متر، بالتالي يمكن تقسيم هذا المربع إلى مربعات صغيرة تحمل مساحات بيكسيلية صغيرة يكون مجموعها عبارة عن متر مربع واحد فقط، وهذا يمكن تبسيطة لو زدنا الأطوال إلى 2 متر فقسمنا الشكل فسيكون لدينا مربع من متر واحد وبجواره مربع من متر آخر ولكن الطول والعرض بسبب زيادته ليصبح مربع واحد ولا يكون عبارة عن معينين متقابلين بالرأس سيتوجب إيجاد مربع يكملان المساحة العامة للشكل وهو متر مربع مجاور للأول ومتر مربع مجاور للآخر وبالتالي ستكون مساحة المربع المكون من أضلاع طولها عبارة عن 2 متر عبارة عن 4 متر مربع لما توضح أعلاه.
لنطور المفهوم وتعريف ومعنى قليلا الآن ونبدأ في عملية إيجاد مساحة المستطيل بالقول أننا نملك مستطيلا طول أضلاعه المتوازية متساوية فقط فسيكون الطول 1 متر والعرض 2 متر، فسيكون المستطيل رأسيا للأعلى وبمجرد أخذ نفس المعاملات التي في الأعلى والتي تكون عبارة عن 1 متر مربع ومن الأسفل 1 متر مربع وبسبب مضاعفة العرض فقط فإنه لن يكون لدينا قيم مكملة للشكل وبالتالي مساحته ستكون 2 متر مربع وهو عبارة عن الطول مضرب بالعرض، أما لو زدنا المفهوم وتعريف ومعنى على سبيل المثال وقلنا أن الطول 2 متر والعرض 3 متر فسيكون المستطيل رأسيا أيضا ولكن سيتم تحليله كالتالي في الأعلى سيكون لدي مربعين من متر مربع واحد وفي الوسط مربعين من متر مربع واحد وبالأسفل مربعين متر مربع واحد وبالتالي مجموعهما سيصبح 6 متر مربع وهو عبارة عن ناتج مضروب الطول في العرض.
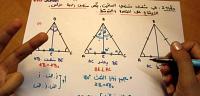
وكذلك الأمر في مساحة شبه المنحرف فهو عبارة عن مثلثين متماثلين من الأطراف ومربع في الوسط، وهذا يدفعنا إلى حساب المربع في الوسط عن طريق تربيع طول الارتفاع لشبه المنحرف ومن ثم إيجاد المثلثين عن طريق ايجاد مساحة المستطيل بضرب القاعدة في الارتفاع للمثلث وتقسيمة على 2 لأن المثلث عبارة عن نصف مساحة المستطيل المعبر عنه في الطرف، ويمكن دمج هاتين العلاقتين الرياضيتين عن طريق القول بأن القاعدة السفلية لشبه المنحرف مجموع لها القاعدة العلوية له سينتج عنه محيط الشكل من الأسفل وعندما نقوم بتقسيمه على 2 سينتج لدينا الوحدة الأساسية المكونة لشبه المنحرف والتي يمكن ضربها في الارتفاع فيما بعد، لتصبح العلاقة الرياضية عبارة عن مجموع القاعدتين مقسوم على 2 مضروب في الارتفاع.