حساب المثلثات
هو علم قائم باسم علم المثلثات أو حساب المثلثات، وهو باللاتينية (Trigonometria)، وهو أحد فروع علم الرياضيات، ويختصّ بدراسة الزوايا والمثلثات وتوابع المثلث على اختلاف نوعه وشكله، ويهتم بالجيب والجيب التمام أو الجتا، ويعدّ علم المثلثات أحد أهمّ فروع علم الهندسة العامة، وقد كان قدماء المصريين أول الدارسين له بقواعده لحساب المثلثات.
استخدم المصريون القدماء هذا العلم لبناء اجمل وافضل عجائب الدنيا والتي حافظت على كيانها لآلاف السنين حتى اليوم؛ الأهرامات والمعابد، لكن وللأسف قليلٌ من موروثهم المكتوب على البردى وصل لنا، ومن العلوم التي وصلت لنا مساحة الدائرة؛ فقد عرفوها بأنها تساوي تسعة أعشار مساحة مربع مرسوم على محيط الدائرة نفسها؛ بحيث تتكون أضلاعها الأربعة من مماسات على محيط الدائرة، مماس لها من أربعة أضلاع، أما ما بني عليه علم حساب المثلثات اليوم فقد استقي من الإغريق، فقد وضعوا قوانينها ووصلت لنا فبني عليها العلم الحديث، ومن أهمّ هذه القوانين هي قوانين المثلث القائم الزاوية والحاد الزاوية، والمنفرج الزاوية.
تطبيقات علم المثلثات
- تخطيط الطرق.
- إنشاء المباني.
- صناعة المحرّكات.
- تصميم أجهزة العرض كالتلفزيون.
- صناعة الأثاث.
- تصميم وتخطيط الملاعب المُختلفة حسب قواعد الألعاب المُختلفة.
- حساب مسافات جغرافيّة وفلك بعيدة.
- حسابات تستخدم لأنظمة الاستكشاف بواسطة الأقمار الصناعية.
قواعد في حساب المثلثات
- يتكوّن مثلثان متشابهان إن كانت فيهما زاويتان متقابلتان متساويتان، وهذا عندما يتشكّل أحدهما من الآخر، بشكل أوضح عند تكبير أو تصغير المثلث، وتكون أيضاً أضلاع هذين المثلثين متناسبة، فمثلاً عندما يكون طول أقصر أضلاع المثلث الأكبر ضعف طول أقصر أضلاع المثلث الأصغر يكون طول الضلعين الأطول والمتوسط في المثلث الأكبر ضعفه بالنسبة للضلعين الأطول والأوسط في المثلث الأصغر.
- إن تساوت زاويتان في مثلثين قائمين؛ فإنّ هذين المثلثين بالضرورة متشابهين، وتكون النسبة متساوية بين الضلعين المقابلين للزاويتين المتساويتين.
المسلمون وعلم المثلثات
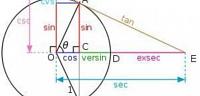
أخذ المسلمون علم المثلثات من الهنود، ليجعلونه علماً خاصاً مستقلاً عن علم الفلك، فأخذوا عن الهنود الجيب، وهو محل وتر ضعف القوس الذي استعمله من قبل اليونانيون.
وكان المسلمون أوّل من أدخل على علم المثلثات الظل أو تعرف ما هو معروف بالمماس، وهو قياس تلك الزاوية المفروضة بالضلع المقابل لها مقسوم على ضلع المثلث المجاور؛ وهذا في المثلث قائم الزاوية، ثم استنبطوا ظل التمام، ودرسوا المثلّثات المستوية والكروية قائمة الزاوية، وعرفوا المثلث القطبي حسب (لوركي).